摘 要

摘　要：通过对高压天然气实际流动状态的分析，结合气体泄漏率模型，求解管道截断阀处的压降速率，为高压天然气管道截断阀爆管检测系统压降速率的设定提供依据。关键词：高压天然气管

摘　要：通过对高压天然气实际流动状态的分析，结合气体泄漏率模型，求解管道截断阀处的压降速率，为高压天然气管道截断阀爆管检测系统压降速率的设定提供依据。

关键词：高压天然气管道  压降速率  泄漏  爆管检测

Setting of Pressure Drop Rate in Pipe Burst Detection System on Natural Gas Pipeline Block Valve

Abstract：Through analyzing the actual flow state of high-pressure natural gas，and based on the gas leakage rate model，the pressure drop rate for pipeline block valve is solved to provide a basis for setting the pressure drop rate in pipe burst detection system on high-pressure natural gas pipeline block valve．

Key words：high-pressure natural gas pipeline；pressure drop rate；leakage；pipe burst detection

 

1　概述

天然气管道常因各种因素如腐蚀穿孔、外部机械撞击、第三方破坏等而导致管内气体发生泄漏。天然气具有易燃、易爆、易扩散的特性，一旦天然气管道发生泄漏，将会带来火灾、爆炸，甚至人员伤亡等严重后果^[1]。

天然气管道截断阀爆管检测系统是用于高压天然气管道爆裂的实时监控系统，主要通过管道压降速率判断管道是否发生爆裂，并可在判断管道发生爆裂后紧急关闭管道截断阀。天然气管道截断阀爆管检测系统大多安装在三、四级地区的管道截断阀上。压降速率设置过高，小的泄漏点监测不到；压降速率设置过低，由于高压管道调峰产生压力变化，可能会造成管道截断阀在正常调峰工况下频繁关闭。由于管道在泄漏工况下压降速率计算复杂，故工程上普遍采用经验值来设定，结果具有很大的不确定性。

为了获得管道在泄漏工况下较为准确可靠的压降速率，本文研究天然气管内气体实际流动状态，即管内气体的瞬态非等温流动状态，并结合气体泄漏率模型，求解管道截断阀处的压降速率，为天然气管道截断阀爆管检测系统压降速率的设定提供依据。

2　管道泄漏物理模型

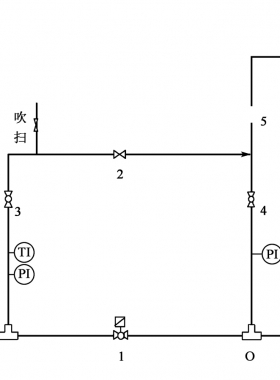
天然气管道泄漏一般为孔口泄漏，如图1所示，管内气体流经孔口的泄漏过程为等熵流动过程。图1中，阀A、阀B为天然气管道的截断阀，泄漏点位于两个截断阀之间，且与阀B的距离为L。

 

该段天然气管道视为固定容积为V的刚性管道，管内气体为一维流动。

管道发生泄漏前后，管内气体均处于非稳态流动状态。管内气体与外界环境存在热量交换，二者间的总传热系数K为常量。管道发生泄漏时，管内气体质量流量保持守恒，即阀A处的气体质量流量等于阀B处的气体质量流量与泄漏气体质量流量之和。在图1中泄漏点处发生泄漏时，气源气流入口(阀A处的温度、压力、流量)均与正常工况相同。

3　管道泄漏模拟数学模型

①连续性方程

气体在管道内流动的连续性方程可由式(1)表示^[2]：

 

式中A——管道的截面积，m²

r——气体密度，kg／m³

t——时间，s

n——气体流速，m／s

x——管道长度，m

由于：

qn=nA      　　　　　　　　　　　　  (2)

 

式中qv——气体体积流量，m³／s

p——管内气体绝对压力，Pa

Z——气体压缩因子

Rg——气体常数，J／(kg·K)

T——气体温度，K

则式(1)变形为：

 

②动量方程

气体在管内流动的动量方程的基础是牛顿第二定律，其表达式^[3]：

 

式中g——重力加速度，m／s²

a——管道轴线与水平面的夹角，弧度

¦——范宁摩擦系数

D——管道内径，m

本文研究的实例为水平管道，a=0，因此式(5)等号右边第1项为0。

③能量方程

能量方程的基础是热力学第一定律，其表达式为^[2]：

 

式中qh——单位质量气体的热交换率，W／kg

cv——气体比定容热容，J／(kg·K)

由于管内气体与外界只发生导热，因此有式(7)成立：

 

式中Ts——土壤温度，K

K——管道综合传热系数，W／(m²·K)

将式(7)代入式(6)并整理，可得到式(8) ^[2]：

 

④泄漏率方程

由于天然气输送管道的压力通常比较高，因此，整个泄漏过程就被分为两个性质不同的阶段，即在泄漏点处气流为亚声速状态的亚临界泄漏阶段和泄漏点处气流为临界状态的临界泄漏阶段^[4]。

当满足式(9)时：

 

式中pa——环境压力，Pa

k——气体等熵指数，天然气取值为1.3

泄漏点处气流处于亚临界泄漏阶段，管道泄漏率方程为式(10) ^[5]：

 

式中qm——管道泄漏率，kg/s

m——流量系数，取0.88～0.90

d——管道泄漏口直径，m

当满足式(12)时：

 

泄漏点处气流处于临界泄漏阶段，管道泄漏率方程为式(12) ^[5]：

 

4　数学模型求解

将上述式(4)、(5)、(8)整理并联立成如下方程绢：

 

将方程组(13)表示成非线性双曲型守恒律形式^[6]：

 

式中

 

采用Crank-Nicolson格式对上式进行离散可得(计算区域网络划分见图2)：

 

 

式中i——计算区域的空间层，即第i空间层

n——计算区域的时间层，即第n时间层

由Taylor展开式得：

 

A为通量E的Jacobian矩阵，其表达式为式(21)：

 

 

式中cp——气体比定压热容，j/(kg·k)

引进符号dUiⁿ⁺¹=Uiⁿ⁺¹-Uⁿi，则式(18)变为式(25)：

 

为了避免式(25)的数值解出现奇偶失联波动并增强格式的稳定性，在右端附加如下四阶耗散项：

 

式中ee⁽⁴⁾——四阶耗散修正系数，取0.1

则式(25)变为：

 

为了保证求解过程的稳定性，在式(26)左端附加如下二阶耗散项：

 

式中ej——二阶耗散修正系数，取0.4

则式(26)可以表示为：

 

式中I——I×I阶单位矩阵

如果存在下述边界条件，则可以简化上述离散后的差分方程组的求解过程：

①左边界(i=1)处存在定值，则有：dU1ⁿ⁺¹=0

②右边界(i=I)处存在：

 

则有：

dUI-1ⁿ⁺¹=dUIⁿ⁺¹

因此，本文采用延长初始时刻和延长出口点数，即在第一时刻之前补充一个l时刻，其各参数均与初始时刻保持一致；管道出口点在原来出口点的基础上增加一个点，即I点，该点参数将与出口点保持完全一致。由于这样并未改变原来管道的运行参数和条件，所得结果也与原来求解结果一致。这样可构成一个三对角方程组，如下：

可采用Tomas开发的TDMA算法对上面的三对角方程组进行求解。TDMA算法可参考相关文献。

 

结合式(32)，已知条件包括管道内径、截断阀A和B间的长度，泄漏点与截断阀B的距离，管道发生泄漏时截断阀A处(计算初始入口边界条件)的气体压力、气体温度、正常工况体积流量、管道外界土壤温度Ts、环境压力Pa、管道总传热系数K、泄漏口直径d等参数，就可以计算出气体某时刻t在管道内某位置x的未知参数：压力P、温度T和流量qV。

本文采用matlab语言进行编程计算，计算中设置的时间步长为1s，空间步长为0.1m。计算步骤为：①通过式(32)，计算出泄漏点处的压力P、温度T和流量qV。②由泄漏点处的压力P等参数，计算泄漏率。③由于管内气体满足质量流量守恒，由前面计算得到的管道泄漏率，就可以计算出流向截断阀B的流量qV，将其与泄漏点处的压力P、温度T一起代入式(32)，就可以计算出t时刻截断阀B处的压力P、温度t和流量qV，从而计算出截断阀B处的管道压降速率dp／dt值。

5　计算案例

以某四级地区高压天然气管道为例，计算不同泄漏点孔径d下截断阀B处的压降速率。

进行计算的高压管道条件为：管道外径0.610m，壁厚11.9mm，内径D为0.586m，截断阀A和B间的长度为8km，泄漏点与截断阀8的距离L为2km。截断阀8上带有爆管检测系统。管道发生泄漏时截断阀A处(计算初始入口边界条件)的气体压力为3.2×100Pa，气体温度为293K，体积流量为22m³／s，气体比定压热容为2.230×10J／(kg·K)。管道外界土壤温度为288K，环境大气压力为101325Pa，管道总传热系数为20W／(m²·K)。

根据上述条件计算，在不同泄漏点孔径d下，截断阀B处的压降逮率情况，计算结果见图3，图中计算起始时间为3s。

 

根据本案例条件高压管道的爆管压降速率计算结果，对于长输管道，考虑其主要承担输气功能，正常运行时各点压力相对稳定，且考虑人工巡线间隔和不同泄漏点的危险程度，建议对于长输管道截断阀爆管检测系统压降速率按不大于d=20mm口径的泄漏压降速率计算值设定。对于城市高压管道，一般既具有输气功能同时又具有日、时调峰功能，正常运行时各点压力变化较大，调峰时段为2.5～4.0h，根据运行经验，调峰时段平均压降速率为125～333Pa／s。对比图3中不同泄漏点直径下的压降速率计算结果，城市高压管道调峰形成的压降速率接近于直径20～30mm的泄漏点造成的压降速率。建议对于城市高压管道截断阀爆管检测系统压降速率按30mm口径泄漏点压降速率设置，对于该管道上小于30mm口径的泄漏点必须靠巡检来发现。

6　结语

对于不同运行工况的天然气高压管道，应根据高压管道的管径、压力、温度、流量等具体的运行工况，并结合管道敷设区域的环境条件，按本文研究的计算方法对爆管压降速率进行计算，作为爆管检测系统设置的参考依据。

 

参考文献：

[1]王剑友．燃气输配系统事故统计分析及对策[J]．煤气与热力，2001，21(2)：178-179．

[2]OSIADACZ A，CHACZYKOWSKI M．Comparison of isothermal and non-isothermal pipeline gas flow models[J]．Chemical Engineering Journal，2000，81(1／3)：41-51．

[3]OSIADACZ A．Simulation and analysis of gas networks[M]．London：E＆F．N．Spoon，1987：58-60．

[4]杨光，谷凯．高压输气管道破裂泄漏事故影响分析[J]．煤气与热力，2008，28(8)：B25-B28．

[5]黄小美，彭世尼，徐海东，等．燃气管道泄漏流量的计算[J]．煤气与热力，2008，28(3)：Bll-Bl6．

[6]张涵信，沈孟育．计算流体力学——差分方法的原理和应用[M]．北京：国防工业出版社，2003：65-72．

 

本文作者：王卫琳  高永和  赖建波  张宝庆  李磊祚  蒋  浩

作者单位：中国市政工程华北设计研究总院