摘 要 由于天然气水合物特殊的理化性质,水合物地层要比常规地层的井壁稳定问题更加复杂,钻井液温度对天然气水合物地层的稳定性影响将是一个不容忽视的因素。为此,考虑热传导、对流、水合物分解、地层力学性质变化等诸多因素及其相互耦合作用,建立了温度影响天然气水合物地层井壁稳定的数学模型,并进行有限元求解。最后以国外某深水天然气水合物地层实际取得的地质资料为例,计算分析了钻井液温度对地层水合物分解、地层力学性质变化及井壁稳定的影响规律。结果表明:地层水合物因受热分解会导致地层力学性质急剧变差,进而极易导致地层屈服失稳,选择低温体系钻井液并控制其温度低于水合物相平衡温度,有助于维持井壁稳定,实现安全钻进。
关键词 天然气水合物地层 钻井液 温度 井壁稳定模型 有限元模拟 地层屈服失稳 相平衡温度
自然界的天然气水合物(以下简称水合物)广泛分布于深水海底、陆地永冻土带和一些内陆湖的深水沉积物中[1-2]。在水合物开采或深水区域油气钻探过程中,水合物地层被打开后,由于钻井液的温度要高于水合物地层温度,水合物稳定存在的相平衡条件被破坏而极易发生水合物分解,进而导致地层力学性质变差,对井壁稳定带来极大的不利影响,直接关系到钻井的成败与成本的高低。国内外对水合物地层的井壁稳定研究还在起步阶段,并且没有实际的经验积累,因此通过模拟的手段对该问题进行研究将具有重要意义。
目前国内外关于钻井液温度对水合物地层井壁稳定影响的研究主要有室内实验和数值模拟两种手段。实验研究多是考虑温度对水合物层的传热及其引起的水合物分解的分析,没有从力学性质的角度来研究井壁稳定的问题[3-5];数值模拟研究往往没有全面考虑温度的影响机制,对地层孔隙中气、水及水合物对导热性质的变化考虑不足[6-7]。在综合考虑热传导、对流及水合物分解吸热等因素的条件下,建立水合物地层能量守恒方程,同时考虑水合物分解动力学、地层流体渗流、井眼附近应力状态及力学性质变化,并考虑这些因素问的互相耦合作用,通过有限元模拟的方法来研究钻井液温度对水合物地层井壁稳定的影响。
1数学模型的建立
1.1 水合物地层能量守恒方程
在考虑热传导、对流、外界能量补给,以及水合物分解吸热等因素的条件下,忽略动能和热辐射,并忽略气体的节流效应和压力对水及水合物热焓的影响,能量守恒方程采用热焓和温度的形式表示为:

式中φ为孔隙度;ρ为密度,kg/m3;H为热焓,J/kg;S为饱和度;ν为流速,m/s;Cp为比热,J/(kg·K);下标r、H、g和w分别代表岩石、水合物、气体和水;Kc为地层有效热传导系数,W/(m·K);Qin为外界的能量补给,J/(m3·s)。
式(1)左边表示系统的内能增量,等式右边第一项表示通过热传导作用进入单位多孔介质系统的能量,等式右边第二项表示外界对水合物地层的热量补给,等式右边第三项表示水合物分解所吸收的能量。
1.2 天然气水合物分解动力学方程
采用Kim-Bishnoi天然气水合物分解动力学模型[9]:

式中mg为单位体积地层天然气的生成速率,kg/(m3·s);Mg为天然气摩尔质量;p为压力,Pa;Φe、Φg分别为天然气在pe和pg下的逸度系数;Adec为单位体积地层内水合物分解表面积,m-1;SH为水合物饱和度;Ahs为单位体积地层比表面积,m-1;Kd0为水合物本征分解速率常数,mol/(m2·Pa·s);ΔE为反应活化能,J/mol;对于甲烷水合物[8],Kd0等于8 060 mo1/(m2·Pa·s),ΔE等于77 330 J/tool;R为气体常数,8.314J/(mol·K);T为温度,K。
1.3渗流方程
假定地层孔隙中含水、气体和水合物三相,只有水和气体两相可以流动。基于连续性方程及广义达西定律等,得到渗流方程:

式中Krg、Krw分别为气和水相对渗透率;[K]为渗透率矩阵,m2;µg、µw分别为气和水的黏度,Pa·s;qg、qw分别为气、水源汇项,kg/(m3·s);g为重力加速度,m/s2;νs为岩石骨架运移速度,m/s;mw为单位体积地层内水生成速率,kg/(m3·s);mH为单位体积地层内水合物分解速率,kg/(m3·s);其他符号意义同前。
1.4应力场方程
根据弹塑性力学理论,得到岩石骨架应力场方程,基于有效应力原理,平衡方程为: ’

式中σij为岩石骨架有效应力,MPa;fi为体力载荷,MPa;ρi为孔隙压力,MPa;a为Biot系数;δij为Kronecker函数。
几何方程的张量形式:

式中εij为应变张量;u为位移。
采用弹塑性本构方程及Drucker-Prager屈服准则,本构方程增量形式:

式中dσij为有效应力增量;Dijkl为弹塑性矩阵张量;dεkl为应变增量。
综合以上水合物地层能量守恒方程、分解动力学方程、地层渗流方程和应力场方程,再辅以相应的辅助方程、初始和边界条件,即构成了完整的水合物地层井壁稳定有限元分析数学模型。
2有限元模拟及结果分析
2.1物理模型及模拟所需参数
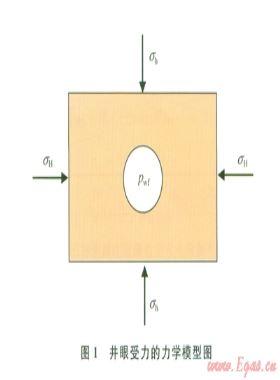
考虑简化的二维平面应变模型,几何尺寸l

渗流场边界条件:BC、CD两边为固定孔隙压力边界,AB、DE两边为自由边界,AE井眼处为井底液压边界。
温度场边界条件:BC、CD两边为固定原始地层温度边界,AB、DE两边为自由边界,AE井眼处为钻井液温度边界。
岩石骨架应力场边界条件:BC、CD两边分别作用最大、最小有效水平地嘘力,AE边为有效井眠液槿压力,AB边为x向滑移边界,DE边为y向滑移边界。
模型内部分布有初始地层孔隙压力、温度和含水合物饱和度。
2.2钻井液温度对地层水合物分解的影响
钻井液温度为本研究的主要因素,取工况为平衡压力钻井,模拟水合物地层打开l h后不同钻井液高于地层的温度差时井壁附近地层的水合物分解情况,结果如图2所示。可以看出,随着钻井液高于地层的温度差越大,井壁附近的水合物分解范围也越大,温差为13 K时水合物分解范围相对4 K时增大了l4.2%。1体积的水合物完全分解可产生164体积的气体[11-12],这些气体进入井筒后将会带来极大的风险,钻井液受到气侵而密度将低,进而导致钻井液柱压力降低,可能造成井壁的垮塌。

从井壁附近地层的温度与水合物饱和度分布(图3)可以看出,钻井液温度向地层传播的范围要大于水合物分解的范围,说明地层中的水合物只有在温度达到能够破坏其相平衡的温度时才会发生分解。控制钻井液的温度低于水合物的相平衡温度,是水合物地层钻井过程中重要的安全保证。

2.3 钻并液温度对地层力学性质的影响
本节分析沿用前面分析的基本模型和条件,研究钻井液温度高于地层温度时引起水合物分解对地层力学性质影响。取地层弹性参数弹性模量和强度参数内聚力来进行分析,各自随钻井液高于地层的温差变化情况如图4、5所示。可见随钻井液温度的升高,地层力学性质变差的区域逐渐扩大。

同时对比水合物饱和度分布图(图2),由于温度升高引起水合物分解,导致地层弹性模量和内聚力大幅降低,力学性质变差。弹性模量由原始地层的6 375 MPa降为4 520 MPa左右,内聚力由原始地层的2 MPa降为水合物分解后的1.5 MPa左右。从图4还还可以看出,在距井眼中心0.2~0.
2.4钻井液温度对井壁稳定的影响
约定地层屈服指数来表征地层的失稳屈服情况,屈服指数等于l时地层为稳定的,屈服指数小于l时地层发生屈服失稳,模拟得到不同钻井液高于地层温差时沿最小水平地应力方向(沿ED边)的屈服指数分布,如图6所示。可见随着钻井液的温度升高,地层失稳屈服的区域增加。与水合物饱和度和地层力学性质变化区域相对应,井壁附近地层水合物由于钻井液的传热作用而发生分解,水合物对地层岩石颗粒的胶结作用减弱,导致地层力学性质变差,地层强度降低,相应的极易发生屈服失稳。
图6
图7为钻井液高于地层温差为7 K时,井眼附近0.
3 结论
1)天然气水合物地层在钻井过程中,钻井液温度对水合物地层的影响是一个极为复杂的物理化学过程,涉及热传导、对流及水合物分解,以及地层应力状态、力学性质的变化,是一个多因素相互耦合的过程,应通过多因素耦合的方法来建立描述该过程的数学模型。
2)随着钻井液高于地层的温度差越大,井壁附近地层的水合物分解范围也越大,同时导致地层的强度降低、力学性质变差,相应地容易发生屈服失稳。并且叠加上非均匀水平地应力的作用,井壁附近地层最小水平地应力方向是屈服失稳的最危险位置。
3)天然气水合物地层钻井过程中,由于井眼液柱压力一般不得低于地层压力,温度是影响地层水合物分解的最主要的因素。基于本数值模拟的分析,可以看出尽量控制钻井液的温度不高于水合物的相平衡温度,能够抑制井壁附近地层水合物的分解,进而有利于保持井壁的稳定。然而,低温又对钻井液的流变性等性能提出了较高的要求,所以优选出能适用于低温环境的钻井液体系,对提高天然气水合物地层的井壁稳定将有很大帮助。
参考文献
[l] 窦斌,REINICKE K M.钻井过程中甲烷水合物的分解特性研究[J].天然气工业,2007,27(12):83-85.
[2] KOH C A.Towards a fundamental understanding of natural gas hydrates[J].Chemical Society Reviews,2002,31:157-167.
[3] 张旭辉,鲁晓兵,李清平,等.水合物沉积层中考虑相变的热传导分析[J].中国科学:物理学力学天文学,2010,40(8):1028-1034.
[4] 张旭辉,刘艳华,李清平,等.沉积物中导热体周围水合物分解范围研究[J].力学与实践,2010,32(2):39-41.
[5] CHAOUCH A,BRIAUD J L.Post melting behavior of gas hydrates in soft ocean sediments[C]//paper 8298-MS-pres-ented at the Offshore Technology Conference,5-8 May,1997,Houston,Texas,USA.Houston:OTC,1997.
[6] RUTQVIST J,MORIDIS G J.Numerical studies on the geomechanical stability of hydrate bearing sediments[C]//paper l8860-MS presented at the Offshore Technology Conference,30 April-3 May,2007,Houston,Texas,USA.Houston:OTC,2007.
[7] KHURSHID l,LEE K J,BAHK J J,et al.Heat transfer and well bore stability analysis in hydrate bearing zone in the east sea,south Korea[C]∥paper 20582 MS presented at the Offshore Technology Conference,3-6 May,2010,Houston,Texas,USA.Houston:OTC,2010.
[8] NAZRIDOUST K,AHMADI G.Computational modeling of methane hydrate dissociation in a sandstone core [J]Chemical Engineering Science,2007,62(22):6155-6177.
[9] KIM H C,BISHNOI P R,HEIDEMAN R A,et al.Kinetics of methane hydrate decomposition[J].Chemical Engineering Science,1987,42(7):1645-1653.
[10] HONG Huifan9.Modeling of gas production form hydrates in porOUS media[D].Calgary:University of Calgary,2003.
[11] XU Wenyue,GERMANOVICH L N.Excess pore pressure resulting from methane hydrate dissociation in marine sediments:a theoretical approach[J].Journal of Geo-physical Research,2006,111:B01104.
[12] NABIL S.Comment on‘Excess pore pressure resulting from methane hydrate dissociation in marine sediments:a theoretical approach’by Wenyue Xu and Leonid N.Germanovich[J].Journal of Geophysical Research,2007,112:78-84.
本文作者:李令东 程远方 梅伟 李清平 高立超
作者单位:中国石油大学(华东)石油工程学院 中海石油研究中心 中国石油长城钻探工程公司固井公司
您可以选择一种方式赞助本站

支付宝转账赞助

微信转账赞助