摘要:研究气流在多孔介质内部的流动特性有助于指导天然气多孔介质燃烧器的设计。为此,对气流在泡沫陶瓷的流动特性进行了冷态实验,研究了气流速度、孔密度对流动阻力的影响,得出在相同空隙率条件下,孔密度与气流速度越大,流动阻力越大的认识;分析了气流分别在颗粒填充床和泡沫陶瓷中流动阻力的产生机理,建立了泡沫陶瓷结构模型,求出了比表面积及空隙率相等(即流动阻力相等)时泡沫陶瓷的孔密度与颗粒填充床颗粒直径间的函数关系,可直接利用制造商提供的泡沫陶瓷的特征参数(孔密度和空隙率),由颗粒填充床经典模型——Ergun方程来预测气流在泡沫陶瓷中的流动阻力,并确定了渗透阻力系数与惯性阻力系数的计算式,借此研究气流在泡沫陶瓷中的流动。实验结果表明,该方法对预测高空隙率的泡沫陶瓷流动阻力是有效的,为进行泡沫陶瓷多孔介质燃烧的数值模拟研究提供了参数计算依据。
关键词:泡沫陶瓷;多孔介质;冷态实验;流动阻力;颗粒填充;渗透阻力系数;惯性阻力系数
目前,天然气燃烧方式主要是以自由火焰为特征的空间燃烧。该燃烧方式温度梯度陡峭且分布不均,局部高温区的存在使得大量N0生成,而且燃烧效率低,燃烧产生的烟气会对环境造成一定污染。天然气在惰性且具有催化作用的多孔介质中燃烧,是一种新型的燃烧技术,能合理利用甲烷,降低污染物排放[1]。相关研究人员对天然气在多孔介质中的燃烧研究集中在高效低污染气体燃烧器、低浓度可燃废气处理和天然气超绝热燃烧富燃制氢反应器的研究[2~12],研究所采用多孔介质的结构形态主要分为颗粒填充与三维网络骨架2种类型,泡沫陶瓷则属于后者。由于多孔介质在强化燃烧、传热的同时,必然增大燃烧器或反应器的流动阻力,将直接影响到燃烧器的设计与运行。因此,研究气流在多孔介质内部的流动具有重要的理论和实际意义。
对于颗粒填充多孔介质中的传热和流动,研究人员开展了广泛的研究。本文参考文献[13]对空气和水流过烧结微细多孔介质内部的流动阻力进行了实验研究和数值模拟,分析了不同颗粒直径条件下摩擦因子与等效雷诺数的关系。本文参考文献[14]基于以Brinkman方程为基础的有效介质方法和一般的点阵模型,研究了固定床层中多孔颗粒内部的流动特性。本文参考文献[15]对学者研究得到的流体流过多孔颗粒填充床的阻力损失计算经验公式进行了总结。但对于三维立体网络骨架和相互贯通气孔结构的泡沫陶瓷近几年才有所研究[15~21]。若采用本文参考文献[15]中总结的经验公式对气流在泡沫陶瓷内部的流动阻力进行计算,最大的难点在于如何建立泡沫陶瓷的网络骨架尺寸与颗粒填充床的颗粒直径之间的关系。而且,由于目前国际上通常用平均每英寸长度上的孔洞数表示其孔洞大小(Pores Per Inch,PPI),即孔密度,泡沫陶瓷制造商一般提供给用户该参数。因此需建立PPI与颗粒填充床颗粒直径间的函数关系,才能应用颗粒填充床经典模型对气流在泡沫陶瓷中的流动阻力进行预测。
基于此,笔者对气流在泡沫陶瓷的流动特性进行了冷态实验研究,研究了气流速度、PPI对阻力的影响;分析了气流分别在泡沫陶瓷和颗粒填充床中流动阻力的产生机理及相似性,建立了泡沫陶瓷结构模型,求出了比表面积及空隙率相等(即流动阻力相等)时泡沫陶瓷的PPI与颗粒填充床颗粒直径间的函数关系,就可直接利用制造商提供的泡沫陶瓷的特征参数(PPI和空隙率),由颗粒填充床经典模型——Ergun方程来预测气流在泡沫陶瓷中的流动阻力。
1 流阻实验装置及方法
图1为气流通过泡沫陶瓷的流动阻力的实验装置图。实验气源由高压氮气瓶提供,通过调整减压阀与阀门的开度可以对气流速度进行控制,以改变实验工况。实验段的压力降和空截面流速采用数字微压差计进行测量。数字微压差计测试范围为-100~+1500Pa,分辨率为0.1Pa,压差精度为±1%读数值。该仪表连接毕托管,即可进行风速测量,测量范围为1~49m/s,精度为±0.07m/s。


图2为泡沫陶瓷及压力测定点布置示意图。用软质材料包裹泡沫陶瓷,放置在钢管中,保证泡沫陶瓷周边与钢管内表面的密封;在钢管侧面开有7个测压孔,其间距为10mm。实验中对测点A与其他6个测点的压力差用数字微压差计进行8次测量,取平均值;空截面风速由毕托管在实验段出口处的不同位置也进行8次测量,取其平均值。实验所采用的泡沫陶瓷规格为50mm×50mm×20mm,PPI分别为10、20、30,空隙率为88%。
2 实验结果与分析
图3是10PPI的泡沫陶瓷在不同风速条件下,流动阻力与测点间距的关系曲线图。横坐标测点间距表示测点A与其他6个测点的距离;纵坐标为相应测点间的压降,即流动阻力。从图3可以看出,多孔介质内的流动阻力随着测点距离、空截面流速的增加而增大。以与测点A距离30mm的测点为分界点,流动阻力与测点距离呈现2种函数关系:测点距离大于30mm时,压力变化与测点距离成正比关系,测点距离小于30mm时,压力变化与测点距离并不符合正比关系。而多孔介质中的流动遵循Forchheimer-Ward关系式:

式中L为测点距离;U为平均流速;μ为流体黏度;K为渗透率;F为二次项系数,由多孔介质的孔径、空隙率等特征参数决定。

由式(1)可以看出,阻力应该与距离成正比。分析造成上述实验现象的原因是:实验中放置泡沫陶瓷的钢管与高压氮气瓶连接需要变径,气流在异径处附近的流速分布不是充分发展紊流,流速分布不对称,有畸变,还可能有漩涡、回流,在测点处的流速偏小,曲线向速度较低的曲线靠近,形成了图3中与测点A的距离小于30mm时的流动阻力形态。因此,在以下分析中,仅对测点距离大于30mm的数据进行分析,即对测点距离小于30mmm的泡沫陶瓷流动进行调整,以此来消除异径对测量结果的影响。
对不同风速下的p-L线性拟合,所得的函数式一次项系数为△p/L。图4为3种孔密度下测试段阻力与风速的关系曲线图。在相同空隙率条件下,孔密度越大,即孔径越小,风速越大,流动阻力越大。采用二阶多项式拟合出流动阻力与速度的关系如图4所示,实验结果遵循关系式(1)。

3 基于Ergun方程的流动阻力模型
气流在多孔介质中的流动阻力主要是由流体质点间存在相互牵制作用、流体与多孔介质的表面摩擦造成的。图5为颗粒填充床示意图。对于气流在颗粒填充床与泡沫陶瓷中的流动,若两者的比表面积及空隙率相等,可认为两者的流动阻力是近似相等的。

颗粒填充床的比面积计算如下:颗粒填充床中有N个直径为d的颗粒,则每个颗粒的表面积为:
Si=πd2 (2)
每个球形颗粒的体积为:
Vi=πd3/6 (3)
设颗粒填充床的空隙率为ε,则在单位体积颗粒填充床中颗粒所占的总体积为:
V=1-ε (4)
单位体积颗粒填充床中的颗粒数为:

由此,单位体积颗粒填充床的总表面(即比面积)为:

图6为泡沫陶瓷结构示意图。泡沫陶瓷是相互贯通的骨架,可简化为立方体结构[16],如图7所示。具体参数计算公式如下:

单元立方体结构体积为:
V0=L3 (7)
单元立方体骨架体积为:
Vs=(1-ε)V0 (8)

则由式(6)、(7)、(8),得:

用n表示每英寸有n个孔,则有:nL=0.0254m。

单元体立方体骨架的表面积为:

泡沫陶瓷比面积为:

由式(10)、(11)、(13)得:

若气流在颗粒填充床与泡沫陶瓷中的流动阻力相当,空隙率和比面积相等,则由式(6)、(14)得:

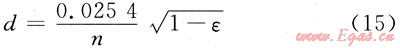
计算颗粒床层阻力采用经典Ergun方程:

式中ρ为气流的密度;μ为气流动力学黏度。
由式(15)与式(16)可知:

若已知孔密度(n)与空隙率(ε),即可对气流通过泡沫陶瓷的流动阻力进行预测。
采用式(17)对笔者研究的泡沫陶瓷(孔径分别为10PPI、20PPI、30PPI,空隙率均为88%)与本文参考文献[18]所研究的泡沫陶瓷(空隙率分别为91.9%、79.4%、68.2%,孔径均为10PPI;空隙率为92.4%,孔径为20PPI)的流动阻力进行预测,并与本文参考文献[14]实验数据对比的结果分别如图8、9所示。从图8、9可以看出,采用式(17)预测气流在泡沫陶瓷中
的流动阻力在PPI较小(即孔径较大、空隙率较大)时与文献实验数据吻合较好。在低空隙率(小于80%)下,预测数值稍有误差,而且空隙率越小误差越大。分析其原因是由于简化的立方体模型与实际的泡沫陶瓷骨架结构不完全一致,空隙率越大其结构越接近立方体模型;空隙率越小其结构越偏离立方体模型,实际流动阻力相对立方体结构模型要大。但由于泡沫陶瓷用于多孔介质燃烧时,所选择的空隙率一般都很大(大于80%)[2~12]。因此该模型能较好地预测气流在泡沫陶瓷中燃烧的流动阻力。

4 渗透阻力系数与惯性阻力系数
进行气体在多孔介质中的燃烧与流动数值模拟时,通常在动量方程中增加1个动量源项来模拟多孔介质的作用。即在简单、均匀的多孔介质上,采用下面的数学模型:

式中α为多孔介质的渗透率,1/α为黏性阻力系数C1;C2为惯性阻力因子。
在模拟多孔介质流动与燃烧时,这2个因子是需要输入的参数条件[22],但以前无经验公式进行计算,一般是采取实验测量或者引用其他文献实验值再进行求解,然而其他文献中的泡沫陶瓷的空隙率与孔径与进行模拟的泡沫陶瓷的空隙率与孔径可能不同,造成模拟研究时存在缺少参数条件的难题。鉴于此,可根据式(17)确定C1、C2分别为:

式(20)、(21)可为模拟工作提供参数计算依据,方便进行泡沫陶瓷多孔介质的燃烧模拟研究。
5 结束语
对气流通过泡沫陶瓷的流动阻力进行了实验研究,发现在相同空隙率条件下,孔密度越大,即孔径越小,风速越大,流动阻力越大;分析了气流在颗粒填充床与泡沫陶瓷中流动阻力产生的机理,得出若两者的比表面积及空隙率相等,可认为两者的流动阻力是近似相等的;基于此,构造了泡沫陶瓷结构模型,求得泡沫陶瓷的PPI与颗粒填充床颗粒直径间的函数关系,可直接采用颗粒填充床经典模型Ergun方程来预测气流在泡沫陶瓷中的流动阻力;将本次实验以及相关文献的实验数据进行了对比,结果表明该方法是有效的。并且可确定出渗透阻力系数与惯性阻力系数,为进行气流在泡沫陶瓷多孔介质中的燃烧数值模拟提供了参数计算依据。
参考文献
[1] 亓新华,谷永庆,王红娟.甲烷催化燃烧催化剂研究进展[J].天然气工业,2007,27(2):125-127.
[2] 许考,张海,樊融.天然气混合催化燃烧污染控制数值研究[J].天然气工业,2008,28(12):101-103.
[3] 杜礼明,解茂昭.预混气体在多孔介质中往复式超绝热燃烧的数值研究[J].燃烧科学与技术,2005,11(3):230-235.
[4] 王恩宇,程乐鸣,骆仲泱,等.天然气在渐变型多孔介质中的预混燃烧启动特性[J].燃烧科学与技术,2007,13(5):393-397.
[5] BHATTACHARYA A,CALMIDI V V.MAHAJAN R L.Thermophysical properties of high porosity metal foams[J].International Journal of Heat and Mass Transfer.2002,45:1017-1031.
[6] ALIE C,FERAUCHE F,LEONARD A,et al.Pd-Ag/Si02 xerogel catalyst forming by impregnation on alumina foams[J].Chemical Engineering Journal,2006,117(1):13-22.
[7] AHN J,EASTWOOD C,SITZKI L,et al.Gas-phase and catalytic combustion in heat-recirculating burners[J].Proceedings of the Combustion Institute,2005,30(2):463-472
[8] 李国能,周昊,钱欣平,等.多孔介质内甲烷超绝热燃烧制氢联合概率密度模拟[J].天然气工业,2007,27(8):112-114.
[9] 杨仲卿,张力,唐强,等.超低浓度煤层气在流态化蓄热装置中的燃烧特性[J].天然气工业,2010,30(6):94-97.
[10] 熊超,秦朝葵,戴万能,等.冷凝式燃气热水器技术及应用[J].天然气工业,2010,30(2):112-114.
[11] 李云清,何鹏,王金成.碳氢燃料在亚临界及超临界状态下的状态方程研究[J].石油与天然气化工,2007,36(1):13.
[12] 周祖鹏.燃烧生命周期影响评价方法的研究[J].石油与天然气化工,2006,35(2):154-157.
[13] 脊蕊娜,姜培学,赵陈儒,等.流体在微细多孔介质中的流动阻力研究[J].工程热物理学报,2007,28(5):841-843.
[14] 高永祥,徐建宽.多孔介质床层中颗粒内部流体的流动[J].天津大学学报:自然科学与工程技术版,2000,33(5):553-559.
[15] MONTILLET A,AKKARI E,COMITI J.About a correlating equation for predicting pressure drops through packed beds of spheres in a large range of Reynolds numbers[J].Chemical Engineering and Processing,2007.46(4):329-333.
[16] 吕兆华.泡沫型多孔介质中非达西流立方框架模型[J].南京理工大学学报:自然科学版,1997,21(1):1-4.
[17] FOURIE J,PLESSIS J.Pressure drop roodeling in cellular metallic foams[J].Chemical Engineering Science,2002,57(14):2781-2789.
[18] DUKHAN NIHAD,PATEL PRAGNESH.Equivalent particle diameter and length scale for pressure drop in porous metals[J].Experimental Thermal and FIuid Science.2008,32(5):1059-1067.
[19] GIANI L,GROPPI G.Mass transfer characterization of metallic foams as supports for structured catalysts[J].Industrial and Engineering Chemistry Research,2005,44(14):4993-5002.
[20] LEONG K C,JIN L W.Characteristics of oscillating flow through a channel filled with open cell metal foam[J].International Journal of Heat and Fluid Flow,2006,27(1):144-153
[21] MAXIME L,PATRICK N,DANIEL S,et al.Pressure drop measurements and modeling on SiC foams[J].Chemical Engineering Science,2007,62(12):3259-3267.
[22] 王恩宇,吴晋湘,刘联胜,等.基于FLUENT对惰性多孔介质中湍流预混燃烧的模拟[J].河北工业大学学报,2007,36(2):94-99.
(本文作者:马培勇1,2 唐志国2 蔡万大1 1.中国科学技术大学;2.合肥工业大学)
您可以选择一种方式赞助本站

支付宝转账赞助

微信转账赞助

