摘 要

根据滑坡体与埋地管道的管—土作用原理，提出横向滑坡和纵向滑坡条件下管道外载的计算方法，基于壳单元和土弹簧单元，建立两种工况下管道的有限元计算模型。

 摘　要：根据滑坡体与埋地管道的管—土作用原理，提出横向滑坡和纵向滑坡条件下管道外载的计算方法，基于壳单元和土弹簧单元，建立两种工况下管道的有限元计算模型。管道受拉压作用而存在三个应力集中区，分别处于两端和中部。除滑坡规模等常规因素外，横向滑坡两侧场地土体性质对管道的受力和变形有明显影响。

关键词：埋地管道；  纵向滑坡；  横向滑坡；　有限元方法；  应力分析

Stress Analysis of Buried Pipeline Subjected to Landslide

Abstract：According to pipeline-soil interactive theory between landslide body and buried pipeline，the calculating method of pipeline external load under the transverse and vertical landslide conditions is proposed．The finite element models of pipeline under the two conditions are built based on shell and spring elements．There are three stress concentration regions at two ends and middle of the pipeline due to tension．The nature of soil at two sides of the transverse landslide has significant influence on stress and deformation of pipeline besides conventional factors like landslide scale．

Keywords：buried pipeline；vertical landslide：transverse landslide；finite element method；stress analysis

 

1　概述

滑坡是输送管道经常遇到的自然地质灾害，滑坡体的滑动使得管道局部产生应力集中并导致断裂破坏，从而影响管道的安全运行。根据滑坡体滑动方向与管道走向所形成交角的变化，管道的外载和潜在失效模式也不尽相同^[1]，通常情况下，国内外学者将其划分为纵向滑坡和横向滑坡^[2-3]。纵向滑坡主要使管道受到轴向摩擦力和向上隆起的垂直作用力，横向滑坡使管道受到垂直于管道轴向与滑坡体滑动方向一致的弯曲作用^[4]。两种情况下的有限元模型考虑因素各异，管道的易受损管段和位置也各不相同，本文提出两种工况下管道外载的计算方法，并建立有限元模型，给出管道的应力分布规律和影响因素，为滑坡区域管道设计施工、应变计安装和应变监测提供参考依据。

2　纵向滑坡

该工况下管道沿山坡方向敷设，管道走向与滑坡体滑动方向一致(见图l)，滑坡体滑动时管道受下滑坡体轴向摩擦作用力明显，另外滑坡体到达底部时受空间限制会发生向上隆起的现象，而在滑坡区域之外，即A、C点以外区域，可以近似认为管道两端受到位移的约束。

 

2.1　有限元模型的建立

采用ABAQUS有限元软件进行应力分析计算，由于管道为薄壁结构，因此可简化采用四边形的壳单元^[5]建模，模型沿管道环向和轴向分别等间距划分单元网格。

管道受到以下作用力：管道内压、输送介质与管道的重力、管道上方土体对管道的压力、管道下方土体隆起时对管道的垂直作用力、周边土体对管道的轴向摩擦力。部分外载计算如下。

①管道上方土体对管道的压力。假设管道的埋深不变，则管道上方土体对管道的压力不随滑坡倾斜角和规模变化，管道上方土体压力为：

pup＝rgh          (1)

式中pup——管道上方土体压力，Pa

r——土体密度，kg／m³

g——重力加速度，m／s²

h——管道埋深，m

②管道下方土体隆起时对管道的垂直作用力。滑坡体到达滑坡底部时由于空间所限，有垂直于管道向上隆起的趋势，采用朗肯理论^[6]建模，其基本原理为处于任意深度的土体压力与计算点到地面的垂直距离d成正比关系，管道不同位置受力不同，任意深度处的土体对管道的压力见式(2)：

pdown＝rgdk0      (2)

式中pdown——下方土体对管道的垂直作用力，Pa

d——计算点到地面的垂直距离，m

k0——土体的压力系数，粘土一般取0.5～0.7，对于砂土可取0.8

③周边土体对管道的轴向摩擦力。沿管道轴向方向，单位长度管道表面所受砂土、粘土摩擦力^[7]150-177分别见式(3.1)、式(3.2)：

Fzf,s＝0.75pDrghm       (3.1)

Fzf,n＝pDassoil          (3.2)

式中Fzf,s——单位长度管道表面管轴方向所受的砂土摩擦力，N／m

D——管道外径，m

m——管—土间的摩擦系数

Fzf,n——单位长度管道表面管轴方向所受的粘土摩擦力，N／m

a——与ssoil有关的经验系数，取值可参考美国ASCE标准^[7]150-177

ssoil——土体剪切强度，Pa

单位长度管道的表面积为,pD，则管道上单位面积所受的砂土摩擦力、粘土摩擦力见式(4.1)、式(4.2)：

fz,x＝0.75rghm    (4.1)

fz,n＝assoil       (4.2)

式中fz,s——管道上单位面积所受的砂土摩擦力，N／m²

fz,n——管道上单位面积所受的粘土摩擦力，N／m²

有限元模型中管道被切为上、下两个部分，两部分受到的内压、管道自身重力及土体摩擦力相同，但两者受到的输送介质重力和土体对管道的垂直作用力应分别考虑，管道两端施加位移约束。载荷分步施加^[8]，第1步：输送介质、管道重力和内压；第2步：土体对管道的垂直作用力；第3步：土体对管道的摩擦力。各类载荷直接施加到壳单元上。

2.2　计算与分析

模型中滑坡体取粘土，土体剪切强度为50kPa，滑坡倾斜角为30°，滑坡规模为25m。以输油管道为例，管道外径为711mm，壁厚为10.3mm，管道材质为X70钢，管道内压8MPa，管道埋深1.8m，管—土间的摩擦系数为0.65。在ABAQUS软件中绘制出管道的Mises应力云图(见图2，单位为MPa)，并沿管道轴向在管道上取A点、B点、C点和经过以上三点的A路径为参考位置和分析对象。

 

由于管道敷设方向与滑坡体滑动方向一致，沿管道轴向的土体摩擦力作用明显，表现在管道下方(A点)受压而上方(C点)受拉，并在A点和C点附近区域形成两个应力集中区。根据朗肯理论，管道下方受到土体垂直作用力，并且随滑坡体下滑而增大，因此管道受到弯曲作用并在管道中部(B点)附近形成第三个应力集中区。总体看来，轴向摩擦力引起的轴向拉压应力和土体垂直作用力引起的弯曲应力两类应力形成组合应力，管道受到组合应力作用表现出相应的应力分布特征。

A路径上各点的垂直方向隆起位移量见图3(其中A点为坐标原点，C点位于管道轴向位置25m处)，可见管道受滑坡体作用发生隆起，且最大隆起位移位于管道中下部，即B点偏下位置，这是因为管道下方受到的土体压力比上方大引起的。

 

将滑坡倾斜角固定为30°，滑坡规模分别为10m、15m、20m、25m和30m，得出管道上最大Mises应力值如表1所示，随着滑坡规模的扩大，管道上的最大Mises应力迅速增大。

 

将滑坡规模固定为25m，滑坡倾斜角分别为15°、20°、25°、30°、35°、40°和45°，A路径上各点的Mises应力值见图4。不同倾斜角下，管道的应力集中区均为管道两端和中下部。但随着滑坡倾斜角的增加，管道的三个应力集中区范围逐渐增大，特别是管道中段的应力集中区向两端延伸，且最大应力值也随之增加。

 

不同滑坡倾斜角时管道隆起位移量见图5。管道的隆起位移量随着倾斜角的增大而增加，但最大隆起位移量始终位于管道中下部，这与管道下方所受土体压力较大有关。

 

3　横向滑坡

该工况下管道走向与滑坡体滑动方向垂直(见图6)，滑坡体滑动时管道主要受滑坡体横向冲刷作用，管道弯曲现象明显，另外还受到轴向拉伸作用。

 

3.1　有限元模型的建立

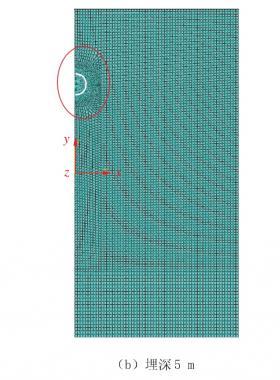
有限元模型的建立与纵向滑坡类似，采用壳单元模拟管道。管道主要受到滑坡两侧场地土体的约束作用力、滑坡体沿滑动方向的横向冲刷作用力、管道上方回填土体的压力、管道内压以及管道和输送介质的自身重力。模拟时，两侧场地土体长度各沿管道轴向取30倍管径^[9]。

土体对管道的作用力可分为轴向摩擦力、水平横向作用力和垂直方向土体压力，均采用土弹簧单元模拟^[10]，每一个壳单元节点附加三个土弹簧(分别代表三个方向的作用力)，土弹簧单元的一端与壳单元连接，另一端施加土体滑动的位移量。随着土体的滑动位移增加，土弹簧对壳单元的作用力线性增加。实际土体与管道相对位移超过一定值后土体发生剪切破坏，对管道的作用力达到极限值后不再随滑坡位移的增加而增加，该极限作用力称为土弹簧的屈服力，相应的位移称为屈服位移。

首先计算土体对单位长度管道的作用力，然后转换为对每一个壳单元的作用力，并施加在土弹簧上；其他类型作用力直接施加在壳单元上。三个方向的土弹簧作用力计算如下。

①管轴方向

管轴方向受土体的摩擦力，单位长度管道表面所受的砂土、粘土摩擦力见式(3.1)、式(3.2)。

将摩擦力分配到有限元模型中各个管轴方向的土弹簧单元，则每个土弹簧单元的屈服力为：

Fz＝FzfL/n　　　　　(5)

式中Fz——土弹簧单元管轴方向所受屈服力，N

Fzf——单位长度管道表面管轴方向所受的砂土或粘土作用力，N／m

L——壳单元管轴方向长度，m

n——管道环向壳单元数量

每个土弹簧单元的屈服位移从密砂土到松砂土为2.54～5.08mm，从较硬粘土到较软粘土为5.08～10.2mm。

②水平横向

水平横向受土体的冲刷作用，水平横向土弹簧主要由土体性质决定。横向土弹簧中土体对管道作用力的极大值为Kennedy方法中的侧向土压力。该值在Et本和美国相关规范中有不同计算公式，这里选取美国ASCE规范，单位长度管道表面在水平横向所受砂土、粘土作用力分别见式(6.1)、式(6.2)：

Fxf,s＝rghNqxD         (6.1)

Fxf,n＝ssoilNcxD        (6.2)

式中Fxf,s——单位长度管道表面水平横向所受砂土作用力，N／m

Fxf,n——单位长度管道表面水平横向所受粘土作用力，N/m

Nqx，Ncx——抗压能力因子，与管道埋深h、管径D、土体性质有关，具体值参考美国ASCE规范^[7]150-177

横向土体作用力分配到有限元模型中的各个水平横向土弹簧单元，则每个土弹簧单元的屈服力及屈服位移分别见式(7)与式(8)：

Fx＝FxfL/n 　　　   (7)

sx＝R0(h+D/2)       (8)

式中Fx——土弹簧单元水平横向所受的屈服力，N

Fxf——单位长度管道表面水平横向所受砂土或粘土作用力，N／m

sx——土弹簧单元水平横向的屈服位移，m

R0——系数，当土体为松砂时，取0.07～0.1；土体为中等密度砂土时，取0.03～0.05；土体为较密砂土时，取0.02～0.03；土体为从较硬到较软的粘土时，取0.03～0.05

③垂直方向

管道在垂直方向主要受到上方土体的压力和下方土体的反力。当管道在竖直平面内移动时，由于地表以上为空，因此管道向上与向下的土体刚度各异，即管道相对于土体向上位移和向下位移时的土体反力不同。因此垂直方向土弹簧单元应分别确定。

a．垂直向上方向

Fyf1,s＝rghNqy1D         (9.1)

Fyf1,n＝ssoilNcy1D        (9.2)

式中Fyf1,s——单位长度管道表面垂直向上方向所受的砂土压力，N／m

Fyf1,n——单位长度管道表面垂直向上方向所受的粘土压力，N／m

Nqy1，Ncy1——抗压能力因子，与埋深h、管径D和土体性质等有关，具体值参考美国ASCE规范^[7]150-177

管道上方土体压力分配到有限元模型中的相应方向土弹簧，则每个土弹簧单元的屈服力和屈服位移分别见式(10)与式(11)：

Fy1＝Fyf1L/n　　　　　(10)

Sy1＝R1h             (11)

式中Fy1——土弹簧单元垂直向上方向所受的屈服力，N

Fyf1——单位长度管道表面在垂直向上方向所受的砂土或粘土的压力，N／m

Sy1——管道上方土弹簧单元垂直方向的屈服位移，m

R1——系数，土体为从密砂到松砂时取0.01～0.05，土体为从较硬到较软粘土时取0.1～0.2

b．垂直向下方向

Fyf2,s＝rghNqy2D+1/2rgD²Nry2      (12.1)

Fyf2,n＝ssoilNcy2D                (12.2)

式中Fyf2,s——单位长度管道表面在垂直向下方向所受的砂土压力，N／m

Fyf2,n——单位长度管道表面在垂直向下方向所受的粘土压力，N／m

Nqy2，Nry2，Ncy2——抗压能力因子，与埋深h、管径D和土体性质等有关，具体值参考美国ASCE规范^[7]150-177

管道下方土压力分配到有限元模型中的相应方向土弹簧单元，则每个土弹簧单元的屈服力和屈服位移分别见式(13)与式(14)：

Fy2＝Fyf2L　　　　　　(13)

Sy2＝R2D             (14)

式中Fy2——垂直向下方向土弹簧单元的屈服力，N

Fyf2——单位长度管道表面在垂直向下方向所受的砂土或粘土压力，N／m

Sy2——管道下方垂直方向土弹簧单元的屈服位移，m

R2——系数，土体为砂土或粘土时取0.10～0.15

对于横向滑坡而言，水平横向土弹簧和轴向土弹簧起主要作用，垂直方向的土弹簧由于管一土相对位移较小作用不大。

管道两端受到滑坡两侧场地土体的约束，中间部分受到滑坡体的冲刷作用，因此在管道两端的轴向方向施加等效弹簧约束，两侧场地土体约束和管道中部的土体冲刷均采用上述的土弹簧模拟。

3.2　计算与分析

模型中滑坡体取粘土，土体剪切强度为50kPa，滑坡倾斜角为30°，滑坡规模为15m，滑坡两侧场地土各取20m。以输油管道为计算对象，管道外径为711mm，壁厚为10.3mm，管道材质为X70钢，管道内压为8MPa，管道埋深1.8m，管—土摩擦系数为0.65。在ABAQUS软件中绘制出管道的Mises应力云图(见图7，单位为MPa)，管道共存在三个应力集中区域(A点、B点和C点)，即管道中部和滑坡体与两侧场地土分界面处的两个弯曲区域，但管段弯曲方向内外两侧由于拉压应力和弯曲应力组合而有所不同，沿管道轴向根据滑坡移动方向在管道两侧选择A路径和B路径为分析对象。

 

绘制出A路径和B路径上管道的Mises应力分布曲线(见图8)，拉压应力和弯曲应力的组合使得管道部分弯曲区域形成最小应力区。

 

计算滑坡规模分别为6m、8m、10m、15m、20m、25m和30m工况下管道的最大Mises应力和最大等效塑性应变(见表2)，随着滑坡规模的不断扩大，管道沿滑坡体滑动方向的应力、应变逐渐增加，当滑坡规模达到一定程度后，管道的应力、应变趋于稳定并开始降低。该现象可以解释当滑坡规模较大时，管道的弯曲程度减缓，使得弯曲应力降低，一定程度上减小了组合应力。

 

为分析滑坡两侧场地土体的影响，以滑坡规模20m为例，其他计算参数不变，分别计算硬土和软土条件下管道的受力情况，硬土和软土的剪切强度分别取50kPa和35kPa，如图9所示，当场地土体为软土(图9-b)时管道横向位移发生范围较长。

 

计算两种情况下管道的最大应力及其位置(见表3)，当场地土较硬时最大应力出现在滑坡体与场地土体交界处，即在A点和B点的弯曲作用明显；而当场地土较软时管道最大Mises应力稍小一些，且最大应力出现在管道的中部，即较软的场地土可以使管道产生更大范围的横向位移，一定程度上缓解了弯曲应力，反而使其最大Mises应力有所降低。

 

4　结论

①根据管道的敷设角度，土体对管道作用力存在较大差别。

②纵向滑坡和横向滑坡工况下管道均存在三个应力集中区域，位于管段两端和中部，但产生原因不同。纵向滑坡条件下管道主要受到土体轴向摩擦力引起的拉压应力和下侧滑坡体的垂直作用力导致的弯曲应力的组合影响；横向滑坡条件下管道主要受到滑坡体的横向冲刷并产生弯曲应力，并由此产生拉应力。受力模式的区别导致两种条件下管道的失效模式稍有不同。

③横向滑坡条件下两侧场地土体性质影响管道的应力和位移分布，设计和施工过程中要适当在潜在滑坡区域两侧的管沟回填软土，以降低滑坡时管道的整体应力值，降低管道的失效概率。

④在管道运营中，对滑坡区域的管道实施应变监测已成为常用的实践手段，根据管道的应力分析结果，应变计应优先布置在滑坡体管段的两侧和中部，而对于纵向滑坡，中部的应变计可适当向下移动以实现与中部应力集中区的重合。

 

参考文献：

[1]刘全林，杨敏．地埋管与土相互作用分析模型及其参数确定[J]．岩土力学，2004，25(5)：728-731．

[2]王沪毅．输气管线在地质灾害中的力学行为研究(硕士学位论文)[D]．西安：西北工业大学，2004：3-8．

[3]张东臣，滑坡条件下埋地管道受力分析[J]．石油规划设计，2001，12(6)：1-6．

[4]邓道明，周新海，申玉平．横向滑坡过程中管道的内力和变形计算[J]．油气储运，1998，17(7)：18-22．

[5]任艳荣，刘玉标，顾小芸．用ABAQUS软件处理管—土相互作用中的接触面问题[J]．力学与实践，2004，26(6)：43-45．

[6]梅国雄，宰金珉．考虑变形的朗肯土压力模型[J]．岩石力学与工程学报，2001，20(6)：851-853．

[7]Committee on Gas and Liquid Fuel Lifelines of the ASCE Technical Council on Lifeline Earthquake Engineering．Guidelines for the Seismic Design of Oil and Gas Pipeline Systems[S]．New York：American Society of Civil Engineers，1984．

[8]朱向荣，王金昌．ABAQUS软件中部分土模型简介及其工程应用[J]．岩土力学，2004，25(2)：144-148．

[9]刘爱文，胡聿贤，赵凤新，等．地震断层作用下埋地管线壳有限元分析的等效边界方法[J]．地震学报，2004，26(1)：141-147．

[10]刘爱文．基于壳模型的埋地管线抗震分析(博士学位论文)[D]．北京：中国地震局地球物理研究所，2002：38-43．

 

 

 

本文作者：焦中良  谷海威  郭杰  刘勇

作者单位：中国石油天然气股份有限公司规划总院

  中国石油天然气股份有限公司天然气与管道分公司